k-nearest-neighbor
Maschinelles Lernen ist aus unserem Alltag nicht mehr wegzudenken. Sei es vom Chatbot bis zur Bilderkennung. Dabei sind die grundlegenden Ideen, die hinter diesen Verfahren stecken gar nicht so schwer zu verstehen. Ein sehr einfaches und anschauliches Beispiel für ein Verfahren des maschinellen Lernens ist das k-Nächste-Nachbarn Verfahren um das es in dem folgenden Text gehen soll.
Der Schwertlilien-Datensatz
Zur Veranschaulichung nutze ich im Folgenden den ziemlich bekannten Iris-Datensatz [1]. In diesem Datensatz sind 150 Schwertlilien der Arten Iris setosa, Iris virginica und Iris versicolor vertreten. Für jeden Eintrag wurde die Blütenblattbreite und Länge, sowie die Länge und Breite der Kelchblätter gemessen. Das Ziel ist nun einen Klassifikator zu bauen. Also einen Algorithmus, der als Eingabe die Länge und Breite der Blüten- bzw. Kelchblätter bekommt und dann zurück gibt, welche Art für diese Angaben am besten passt.
Schauen wir uns zunächst einfach mal die Daten an. Um es nicht zu kompliziert zu machen, fokusieren wir uns vielleicht einfach erstmal auf die Länge und Breite der Blütenblätter. Zur Visualisierung eignet sich hier ein Scatterplot gut. Dabei tragen wir auf der x-Achse die Blütenblattbreite und auf der y-Achse die Blütenblattlänge ab. Jeder Eintrag wird dann als eigener Punkt im Diagramm abgetragen. Zusätzlich färben wir die Punkte je nach Art ein:
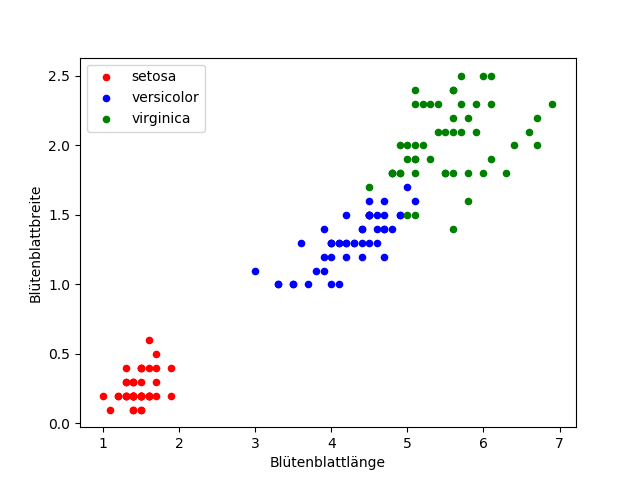
Wenn wir diesen Scatterplot betrachten fällt uns sofort etwas auf: die verschiedenen Arten formen in ihrer Merkmalsausprägung ein Cluster. So liegt die Blütenblattlänge für Iris setosa zwischen etwa 1 und 2 cm und die Blütenblattbreite bei der gleichen Art zwischen 0,2 und etwa 0,6 cm. Da kann man schon recht schnell auf die Frage kommen, ob wir uns diese Tatsache zu nutze machen können? Dazu gleich mehr.
Doch davor schauen wir uns noch einmal die anderen Merkmale an. Da wir hier nur vier Merkmale haben, eignet sich dafür eine Scatterplotmatrix ganz gut. Dabei wird für jede der 6 möglichen Kombinationen an zwei Merkmalen ein eigener Scatterplot erstellt und gemeinsam in einer Matrix abgetragen:
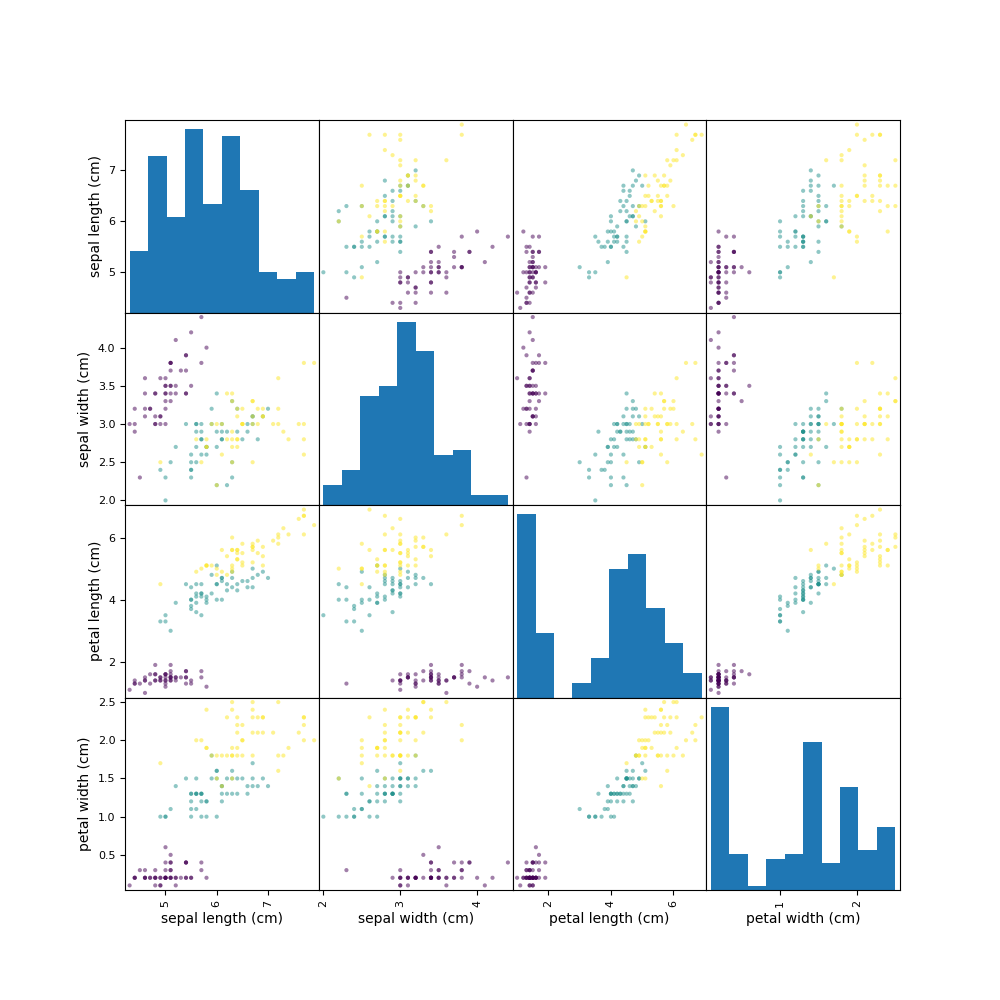
Die Diagonaleinträge können wir für unsere Zwecke ignorieren. Auch fällt auf, dass hier 12 statt 6 Scatterplots abgetragen sind. Allerdings sind bei allen Einträgen links der Diagonale einfach nur die Achsen vertauscht. Unabhängig davon fällt auf, dass auch in den anderen Merkmalen diese Clusterbildung sichtbar ist. Das sollte sich doch wirklich ausnutzen lassen…
Das Funktionsprinzip des k-Nächste-Nachbar Klassifikator
Bevor wir uns konkret mit dem Iris-Datensatz beschäftigen schauen wir uns doch einfach nochmal die Theorie an einem künstlichen Beispiel an. In der folgenden Abbildung haben wir zwei verschiedene Kategorien gegeben: blaue Kreuze und orangene Punkte.
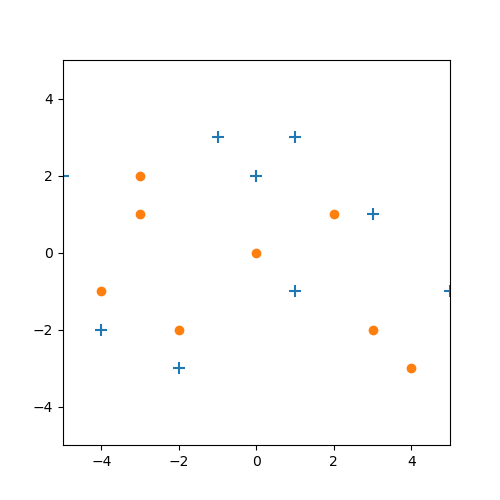
Nehmen wir nun an, dass wir einen weiteren Datenpunkt hinzu bekommen, und zwar das grüne Dreieck, und diesem eine Kategorie zuordnen möchten.
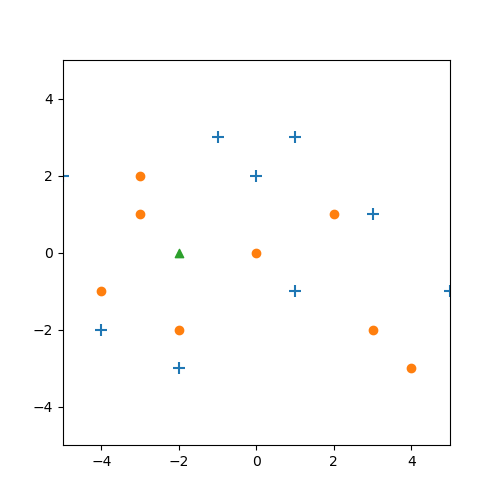
Wie können wir vorgehen? Nun, ein naheliegender Vorschlag wäre, uns die $k$ Nachbarn anzusehen, die zu dem neuen Datenpunkt den geringsten Abstand haben.
Wenn wir in unserem Beispiel mal $k=3$ setzen bekommen wir die folgende Situation:
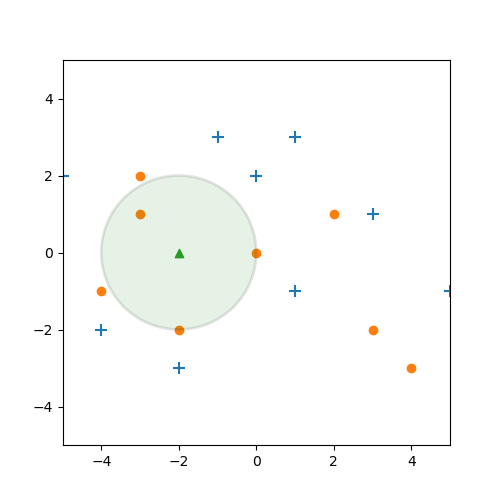
Wir sehen also, dass die nächsten drei Nachbarn, orangene Punkte sind. Demzufolge sollte unser neues Objekt auch ein orangener Punkt sein.
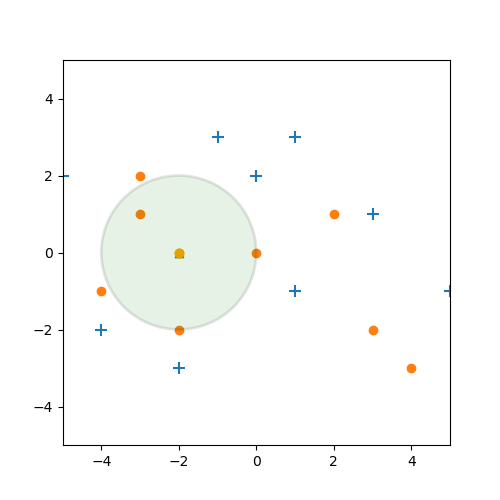
Anderes sieht die folgende Situation aus:
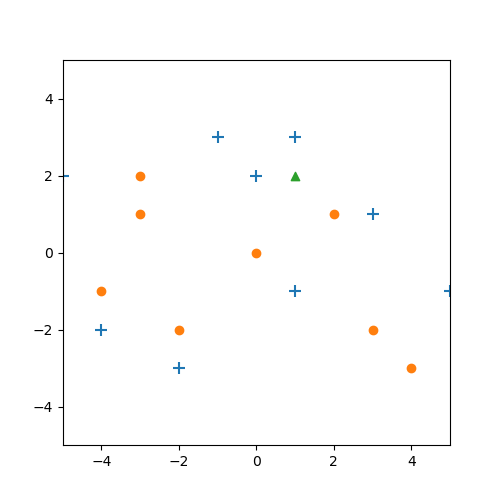
Schauen wir uns hier die nächsten drei Datenpunkte an, stellen wir fest, dass 2 blaue Kreuze und ein orangener Punkt dabei sind. Welches Label sollen wir hier vergeben? Nun, am einfachsten ist das Label, welches unter den nächsten drei Nachbarn am häufigsten vorkommt. Also hier das blaue Kreuz.
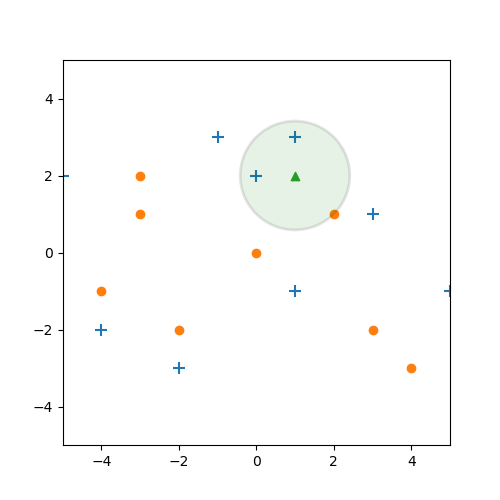
Ein letztes Beispiel:
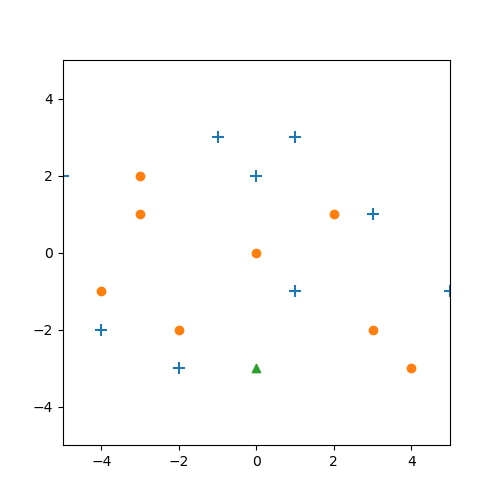
Hier passiert etwas interessantes. Zunächst die Situation für $k=3$. Die ist nicht weiter besonders, da wird wie im vorherigen Beispiel ein blaues Kreuz vergeben.
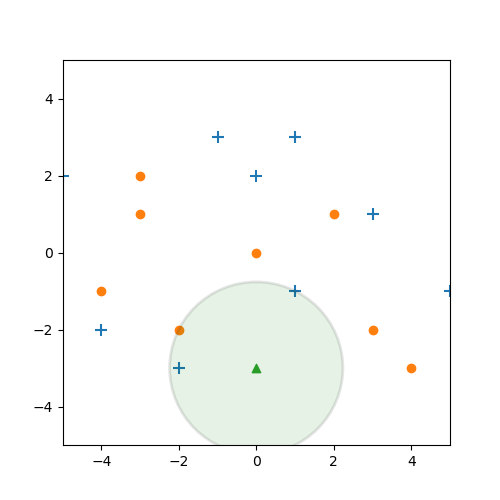
Aber würde passieren, wenn wir uns statt der nächsten drei, die nächsten $k=5$ Elemente ansehen?
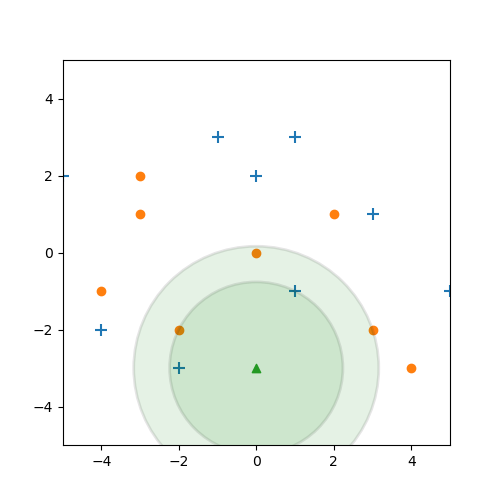
Dann stellen wir auf einmal fest, dass wir 2 blaue Kreuze und 3 orangene Punkte haben. Bei einer Mehrheitsentscheidung, würde der Datenpunkt also als orangener Punkt klassifiziert werden.
Wir stellen also fest, dass das Ergebnis von unserem $k$ abhängt. Ein sogenannter Parameter von unserem Maschinellem Lernproblem. Die optimalen Werte für solche Parameter zu bestimmen ist eine große Aufgabe in der Entwicklung von so einem System. Dazu aber im nächsten Abschnitt mehr.
Referenzen
- R. A. Fisher (1936). “The use of multiple measurements in taxonomic problems”. Annals of Eugenics. https://doi.org/10.1111/j.1469-1809.1936.tb02137.x