Pi mit Hilfe des Zufalls bestimmen
Bekanntlich beträgt der Flächeninhalt eines Kreises mit Radius $r$ $A_K = \pi r^2$. Wir betrachten nun einen Inkreis eines Quadrates, also den Kreis der im Inneren eines Quadrates liegt und das Quadrat genau in den Mittelpunkten der Kanten berührt. Dargestellt ist diese Situation in der folgenden Abbildung:
Dieses Quadrat hat nun eine Kantenlänge von $l=2r$ und damit einen Flächeninhalt von $A_Q=4r^2$. Der Anteil des Kreises im Vergleich zur Gesamtfläche des Quadrates beträgt also damit $\frac{A_K}{A_Q} = \frac{\pi}{4}$.
Das interessante ist nun, dass wir mit diesem Wissen den Wert von $\pi$ recht gut abschätzen können. Die grundlegende Idee ist die folgende: Wir wählen in dem Quadrat zufällig einen Punkt. Unter der Vorraussetzungen, dass alle Punkte in dem Quadrat die gleiche Wahrscheinlichkeit hat, gewählt zu werden (der Mathematiker spricht dann von einer uniformen Verteilung oder Gleichverteilung), liegt der Punkt mit einer Wahrscheinlichkeit von $\frac{\pi}{4}$ innerhalb des Kreises.
Jetzt wählen wir aber nicht nur einen Punkt in dem Quadrat sondern viele nacheinander und unabhängig von einander. Dabei zählen wir, wie viele der Punkte innerhalb des Kreises liegen. Nun hilft uns die Wahrscheinlichkeitstheorie, denn laut dem Gesetz der großen Zahlen nähert sich der Anteil der im Kreis liegenden Punkte genau $\frac{\pi}{4}$ an. Das heißt für große $n$ gilt $\frac{\text{Punkte im Kreis}}{n} \approx \frac{\pi}{4}$. Man muss nun also nur noch beide Seiten mit vier multiplizieren und erhält eine recht gute Abschätzung für $\pi$. Wichtig ist: $\frac{\text{Punkte im Kreis}}{n} = \frac{\pi}{4}$ gilt nur, wenn $n\rightarrow \infty$, also wenn $n$ unendlich groß wird. Theoretisch ist es schließlich möglich, dass auch die ersten $1000000$ Punkte außerhalb des Kreises liegen. Allerdings ist dieser Fall sehr unwahrscheinlich.
Genug der grauen Theorie. Führen wir das Experiment einmal praktisch durch. Um es einfach zu halten, nutzen wir einen Einheitskreis mit Radius $r=1$. Das entsprechende Quadrat hat also eine Kantenlänge von $l=2$. Jetzt ziehen wir zufällig aber gleichverteilt $1000$ Punkte:
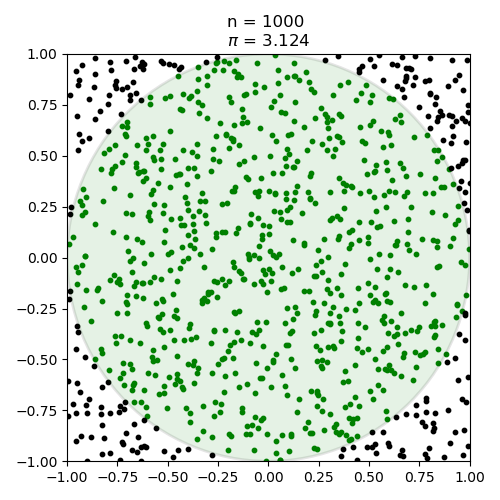
Wenn wir zählen würden, würden wir feststellen, dass 781 unserer Punkt im Kreis liegen. Demzufolge gilt $\pi \approx 4\cdot\frac{781}{1000} = 3.124$. Das ist sicherlich eine Näherung von $\pi$ aber weit weg von perfekt. Wir können das Experiment ja mit verschieden großen Werten von $n$ durchführen. Das ist im Folgenden passiert. Dabei variierte $n$ zwischen $100$ und $1000000$. Der Wert von $\pi$ ist dabei im folgenden Diagramm mit der rot gestrichelten Linie eingetragen:
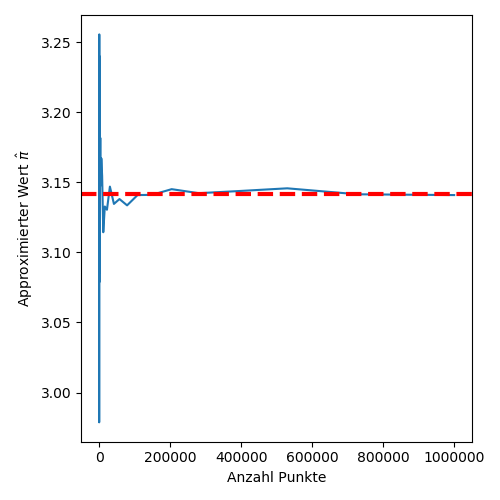
Schaut man sich den Betrag des Fehlers an, sieht man, dass mit dieser Methode ab etwa $1000000$ Punkten $\pi$ auf zwei Nachkommastellen genau abgeschätzt wird.
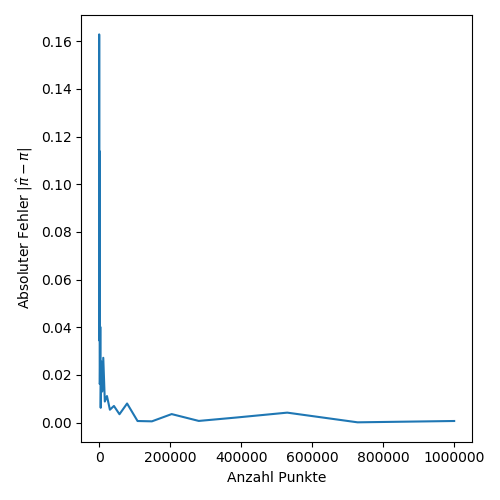
Sehr viel besser wird das Ergebnis aber leider nicht. Denn selbst bei $10000000$ Punkten, wird $\pi$ nur auf etwa 3 Nachkommastellen genau berechnet. Das zeigt auch sehr schön den Nachteil dieser Methode in der Praxis. Für eine beliebig genaue Approximation von $\pi$ sind so viele Punkte notwendig, dass es nicht mehr praktikabel umsetzbar ist. Denn für $k$ Nachkommastellen sind mindestens $10^k$ Punkte notwendig, in der Realität aber mehr, denn wir haben ja noch den Zufall mit im Spiel. Dafür ist dieses Vorgehen sehr anschaulich und gut verständlich im Vergleich zu den effizienteren aber auch komplizierteren Methoden. Allerdings findet diese Methode, die übrigens Monte-Carlo-Methode genannt wird, in vielen anderen Bereichen der Statistik und darüber hinaus seine Anwendung.
Literatur
- Christopher M. Bishop: Pattern Recognition and Machine Learning, Springer, 2006, ISBN 978-0-387-31073-2